Rruga e Eulerit
Në teorinë e grafeve, një rrugë e Eulerit në një graf është rruga e cila secilën nyje të grafit e viziton vetëm një herë. Cikël i Eulerit është rruga e Eulerit e cila mbaron në të njëjtën nyje prej ku ka filluar. Këtë lloj grafesh e studioj Leonhard Euler kur e zgjidhi problemin e famshëm të shtatë urave të Königsbergut në vitin 1736. Matematikisht problemi i shtatë urave formulohet si më poshtë:
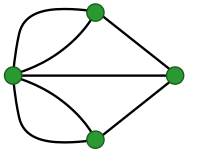

- Është dhënë grafi në të djathtë, A është e mundur të konstruktohet rrugë ose cikël e cila fillon dhe mbaron në të njejtën nyje dhe secilën prej nyjeve tjera e viziton vetëm një herë?
Euleri vërejti se kusht i nevojshëm që një graf të ketë rrugë ose cikël të Eulerit është që ç'do nyje e tij të jetë e shkallës çift me fjalë tjera nga ç'do nyje del një numër çift degësh; Kjo do të thotë se grafi i Königsbergut nuk është Eulerian.
Referimet
Redakto- Euler, L., "Solutio problematis ad geometriam situs pertinentis", Comment. Academiae Sci. I. Petropolitanae 8 (1736), 128-140.
- Hierholzer, C., "Über die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechnung zu umfahren", Mathematische Annalen 6 (1873), 30-32.
- Lucas, E., Récréations Mathématiques IV, Paris, 1921.
- Fleury, "Deux problemes de geometrie de situation", Journal de mathematiques elementaires (1883), 257-261.