Fusha magnetike

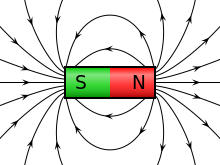
Në fizikë, një fushë magnetike është një fushë vektoriale që përshkon gjithë hapësirën dhe e cila shkakton një forcë magnetike mbi një ngarkesë elektrike lëvizëse ose mbi një dipol magnetik (siç janë magnetet e përhershëm). Kur vendoset në një fushë magnetike, dipoli magnetik tenton që të drejtohet sipas një boshti që është paralel me fushën magnetike, siç mund të shikohet edhe nga pluhuri i hekurit në prezencën e një magneti (shikoni pikturën në të djathte). Për më tepër, një fushë magnetike që ndryshon në kohë shkakton induktimin e një fushë elektrike. Fushat magnetike rrethojnë dhe në të njëjtën kohë kanë si burim korrentet elektrike, dipolët magnetike, dhe fushat elektrike që ndryshojnë në kohë. Fushat magnetike mbartin energjinë e tyre, një denitet energjie e cila është në përpjesëtim të drejte me intensitetin e fushës. Forca magnetike shkruhet me inicjalet M+

Fenomeni i fushës magnetike shfaqet në disa raste specifike. Për fiziken e materialeve magnetike shikoni artikujt mbi magnetizimin dhe magnetin, ose me specifikisht ferromagnetizmi, paramagnetizmi, dhe diamagnetizmi. Për fusha magnetike konstante, si ato te prodhuara nga dipole stacionare ose nga korrente të qëndrueshëm, shikoni artikullin mbi magnetostatikën. Për fusha magnetike të krijuara nga fusha elektrike që ndryshojnë në kohë shikoni artikullin mbi elektromagnetizmin.

Fusha elektrike dhe fusha magnetike janë dy fusha shumë të ndërlidhura me njëra tjetrën, ne të dyja drejtimet. Se pari, ndryshime në secilën nga këto dy fusha shkaktojnë ("induktojnë") ndryshime tek fusha tjetër, sipas ekuacioneve te Maksuellit. Se dyti, sipas teorisë së relativitetit special të Ajnshtajnit, një forcë magnetike në një sistem referencë inerciale shihet si një forcë elektrike në një sistem tjetër nga një observues në atë sistem, or vice-vërsa (shikoni elektromagnetizmi relativist për shembull). Së bashku, ato dy fusha përbejnë fushën elektromagnetike, e cila është koncepti themelor për shpjegimin e dritës dhe valëve elektromagnetike.

Përkufizimet, njësitë, dhe matja

Fusha B

Fusha magnetike mund të përkufizohet në disa mënyra ekuivalente duke u bazuar në efektet që ka në mjedis.

Shpesh fusha magnetike përkufizohet si forcë që i bën ngarkesat të lëvizin. Është e njohur nga eksperimentet në elektrostatikë se nëse kemi një ngarkesë pikësore q në një fushë elektrike E atëherë shfaqet forca F = qE. Sidoqoftë, në situate tjera, kur ngarkesa pikësore lëvizë në afërsi të një kablloje rrymë-mbajtëse, forca varet edhe nga shpejtësia e asaj ngarkese. Fatmirësisht, pjesa e varuar nga shpjetësia mund të ndahet ashtu që forca përshkruhet sipas Ligjit të Lorcencit,

$\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ).$

Këtu v paraqet shpejtësinë ndërsa x është produkti vektorial. Vektori B cilësohet si fushë magnetike dhe definohet si vektori i fushës i nevojshëm për ta bërë ligjin e Lorencit të saktë në përshkrimin e nocionit të ngarkesës pikësore. Ky definimi lejon përcaktimin e B-hit në këtë mënyrë^[1]

   Merret një pjesë e njohur e ngarkesë q. Përdoret forca në atë ngarkesë për të përcaktuar fushën E. Pastaj matet forca në atë pjesë kur shpejtësia është v; përsëritet me v në disa drejtime. Tani gjindet B që bën të përshtatet të gjitha rezultatet – kjo është fusha magnetike në atë vend.

Fusha H

Përvec B-hit, ekziston edhe H-hi, i cili po ashtu quhet fushë magnetike. Në vacuum, B dhe H janë proporcionale njëra me tjetrën, me një konstantë e varur nga njësitë fizike. Brenda materialit ato janë të ndryshme. Termi “fushë magnetike” është historikisht e rezervuar për H ndërkohë që përdoren terma të tjerë për B. Joformalisht, edhe pse edhe formalisht në disa libra të fizikës, termi “fushë magnetike” përdoret për të përshkruar B-hin ashtu sikur H-hi apo të vend të H-hit. Ka mjaft emra alternative për të dyja.

Njësitë

Në sistemin SI, njësia për B-në është tesla (simboli: T) dhe fluksi magnetik njehsohet me veber (simboli: Wb) kështu që densiteti i fluksit 1 Wb/m2 është 1 tesla. Në sistemin SI, njësia tesla është ekuivalente me (njuton·sekond)/(kulon·metër). Në sistemin CGS, B njehsohet me gaus (simboli: G). (Konvertimi është 1 T = 10,000 G.) Fusha H njehsohet me amper për metër (A/m) në sistemin SI, dhe me oersteds (Oe) në njësitë cgs. ^[2]

Matja

Pajisjet që përdoren për matjen e fushës locale magnetike quhen magnetometra. Klasët e rëndësishme të magnetometrave përfshijnë përdorjen e spiraleve rrotulluese, magnetometrat Hall effect, NMR, SQUID, dhe magnetometrat fluxgate. Fushat magnetike të objekteve të largëta astronomike maten përmes efekteve të tyre në ngarkesa pikësore. Për shembull, elektronet që rrotullohen rreth një vije fushe prodhojnë rrezatim sinkrotron që është e detektueshme në valët e radios.

Vijat e fushës magnetike

Kompasët tregojnë drejtimin e fushës locale magnetike. Siç shihet këtu, fusha magnetike tregon kah poli jugor i magnetit dhe në anën e kundërt të polit verior.

Përcaktimi i fushës magnetike të një objekti është i thjeshtë në parim. Fillimisht, matet fortësia dhe drejtimi i fushës magnetike në një numër të madh të lokacioneve (ose në secilën pikë në hapësirë). Pastaj, shënohet secili lokacion me një shigjetë (të quajtur vektor) që tregon në drejtim të fushës locale magnetike me madhësi proporcionale me fortësinë e fushës magnetike.

Si metodë alternative për përcaktimin e fushës magnetike është të “lidhen” shigjetat për krijimin e vijave të fushës magnetike. Drejtimi i fushës magnetike në çdo pikë është afërsisht paralel me vijat e fushës dhe densiteti local i vijave të fushës mund të proporcionalizohet me fortësinë e tyre.

Vijat e fushës magnetike janë si kontura vijash (lartësi konstante) në një hartë topografike ku prezantojnë diçka të vazhdueshme dhe një tjetër shkallë e paraqitjes do të tregonte më shumë ose më pak vija. Një avantazhë i përdorimit të vijave të fushës për paraqitjen e fushës magnetike është për shkak se shumë ligje të magnetizmit (dhe elektromagnetizmit) mund të thuhen plotësisht dhe në mënyrë të prerë duke përdorur koncepte të thjeshta si “numri” i vijave të fushës në një sipërfaqe. Këto koncepte mund të “përkthehen” lehtë në formë matematikore. Për shembull, numri i vijave të fushës në një sipërfaqe të dhënë është një integral i syprinës i fushës magnetike.

Drejtimi i vijave të fushës magnetike e paraqitur nga rreshtimi i pluhurit të hekurit të vendosura në një letër mbi një magnet.

Fenomene të ndryshme kanë efektin e “paraqitjes” së vijave të fushës magnetike megjithëse vijat e fushës janë fenomen fizik. Për shembull, pluhuri i hekurit i vendosur në fushë magnetike formon vija që i korrespondojnë “vijave të fushës”. “Vijat” e fushës magnetike janë po ashtu të shfaqura vizualisht në aurorat polare, ku dipoli grimcor i plazmës ndërvepron duke krijuar vija të dukshme të dritës që rreshtohen me drejtimin e vijave të fushës magnetike të Tokës.

Vijat e fushës mund të përdoren si mjet cilësor për të vizualizuar forcat magnetike. Në substancat ferromagnetike si hekuri dhe në plazma, forcat magnetike mund të kuptohen duke imagjinuar se vijat e fushës shfaqin një tension (si një band gome) përgjatë gjatësisë së tyre, dhe një shtypje pingule me gjatësitë e tyre në vijat fqinje të fushës.

Fusha magnetike dhe rrymat elektrike

Rryma e ngarkesave elektrike gjeneron një fushë magnetike dhe paraqitet ndjesia e forcës për shkak të B-fushave magnetike.

Fusha magnetike për shkak të lëvizjes së ngarkesave dhe rrymave elektrike

Rregulla e dorës së djathtë: rryma rrjedh në drejtim të shigjetës së bardhë prodhon një fushë magnetike të treguar nga shigjeta e kuqe.

Të gjitha grimcat në lëvizje prodhojnë fushë magnetike. Çdo pikë ngarkese, si elektronet, prodhojnë fushë të komplikuar, por të njohur, magnetike, që varet nga ngarkesa, shpejtësia dhe nxitimi i grimacave.

Vijat e fushës magnetike kanë formën e rrathëve koncentrik rreth përçuesit rrymë-mbajtës cilindrik, si një kabllo e gjatë. Drejtimi i një fushe të tillë mund të përcaktohet duke përdorur “rregullën e dorës së djathtë” (shih figurën djathtas). Fortësia e fushës magnetike bie me distancën nga kablloja (për gjatësi të pakufishme të kabllos fortësia është anasjelltas proporcionale me distancën).

Solenoidi

Lakimi i kabllos rrymë-mbajtëse në harqe koncentron fushën magnetike brenda harkut duke e bërë të dobët jashtë. Duke lakur kabllon në hapësira të ngushta për të krijuar një spirale ose “solenoid” e rrit këtë efekt. Një pajisje e formuar rreth një kablloje të hekurit mund të sillet si një electromagnet, duke gjeneruar një fushë magnetike të fortë dhe të kontrolluar mirë. Një electromagnet i gjatë cilindrik ka një fushë magnetike uniforme përbrenda dhe nuk ka fushë magnetike jashtë. Elektromagneti me gjatësi të kufishme prodhon një fushë magnetike që duke e ngjashme me atë që e kirjojnë një magnet permanent uniform, me fortësinë e tij dhe polaritetin e përcaktuar nga rryma që rrjedh nëpër spirale.

Fusha magnetike e gjeneruar nga një rrymë e qëndrueshme I (rrjedhje konstante e ngarkesës elektrike, ku ngarkesa nuke ndryshon në asnjë pikë) është e përshkruar me ligjin e Bio-Savarit:

\mathbf {B} ={\frac {\mu _{0}I}{4\pi }}\int _{\mathrm {wire} }{\frac {d{\boldsymbol {\ell }}\times \mathbf {\hat {r}} }{r^{2}}},

Ku nën integral është gjatësia e kabllos ku vektori dl është vektori elementar me drejtim të njëjtë me rrymën I, mu është konstanta magnetike, r është distance në mes të vendit ku ndodhet dl dhe vendit ku po llogaritet fusha magnetike dhe r është vektori njësi në drejtim të r.

Në formë më të përgjithësuar, rruga e rrymës I në fushën B gjendet përmes Ligjit të Amperit:

\oint \mathbf {B} \cdot d{\boldsymbol {\ell }}=\mu _{0}I_{\mathrm {enc} },

ku integrali linjor është mbi gjitha harqet dhe Ienc është rryma e tërë harqeve. Ligji i Amperit është gjithmonë i vlefshëm për rryma të qëndrueshme dhe mund të përdoret për të llogaritur fushën B për situate tërësisht simetrike si kabllo infinite ashtu edhe solenoid infinit.

Në një formë të modifikuar, ligji i Amperit është një nga katër ekuacionet e Maksuellit që përshkurajnë elektricitetin dhe magnetizmin.

Forca në ngarkesat lëvizëse dhe rryma

Drejtimi i ngarkesave pikësore në fushë magnetike (A) pa forcë përfundimtare, (B) fushë elektrike, E, (C) një ngarkesë e pavarur nga forca, F (p.sh. graviteti), dhe (D) një fushë magnetike johomogjene, grad H.

Forca në ngarkesë pikësore

Ngarkesa pikësore që lëviz në fushën B përshkruan një forcë anësore që është proporcionale me fortësinë e fushës magnetike, komponentën e shpejtësisë që është normale në fushën magnetike dhe ngarkesën pikësore. Forca është e njohur si Forca e Lorencit, dhe është e dhënë sipas:

\mathbf {F} =q\mathbf {v} \times \mathbf {B} ,

ku F është forca, q është ngarkesa pikësore elektrike, v është shpejtësia e çastit e ngarkesës, dhe B është fusha magnetike (në tesla).

Forca e Lorencit është gjithmonë normale, tek shpejtësia e ngarkesës dhe tek fusha magnetike që ajo krijon. Kur ngarkesa pikësore lëviz në fushë magnetike statike, ajo ndjek një rrugë spirale ku boshti spiral është paralel me fushën magnetike, dhe ku shpejtësia e grimcës mbetet konstante. Për shkak se forca magnetike është gjithmonë normale në lëvizje, fusha magnetike nuk mund të kryej punë në një ngarkesë të izoluar. Ajo vetëm mund të kryej punë në mënyrë indirekte, përmes fushës elektrike të gjeneruar nga një fushë magnetike e ndryshuar. Shpesh sqarohet se fusha magnetike mund të kryej punë tek një dipol magnetik jo-elementar, ose te një ngarkesë pikësore lëvizja e së cilës udhëhiqet nga forca të tjera, por kjo nuk është e saktë^[3] sepse puna në këto raste është shfaqur nga forcat elektrike të ngarkesave të shtrembëruara nga fusha magnetike.

Forca në kabllon rrymë-mbajtëse

Forca në kabllon rrymë-mbajtëse është e ngjashme me atë të një ngarkese në lëvizje të supozuar pasi kablloja e tillë është një grumbull i ngarkesave lëvizëse. Kablloja rrymë-mbajtëse ndjen një forcë në prezencë të fushës magnetike. Forca e Lorencit në një rrymë makroskopike shpesh referohet si Forca e Laplasit. Të konsiderojmë një përçues të gjatësisë l, prerja tërhore A, dhe ngarkesa q për shkak të rrymës elektrike i. Nëse ky përçues është i vendosur në një fushë magnetike B që krijon një kënd teta me shpejtësinë e ngarkesave në përçues, forca në një ngarkesë të vetme q është

F=qvB\sin \theta ,

kështu që për N-ngarkesa, ku

N=n\ell A

,

forca në përçues është

f=FN=qvBn\ell A\sin \theta =Bi\ell \sin \theta

,

Ku i=nqvA.

Rregulla e dorës së djathtë: gishti i madh tregon rrymën dhe gishtat e tjerë tregojnë drejtimin e B-së, forca tregohet nga shuplaka lart. Forca është e ngarkesës negative.

Drejtimi i forcës

Drejtimi i forcës në një ngarkesë ose rrymë mund të përcaktohet nga një mnemonic të njohur si rregulla e dorës së djathtë (shih figurën). Duke përdorur rregullën e dorës së djathtë dhe duke treguar me gisht të madh në drejtim të lëvizjes së ngarkesave positive ose rrymës positive dhe gishtat tjerë në drejtim të fushës magnetike, forca rezultuese shfaqet nga shuplaka lart. Forca në ngarkesën pikësore negative është në drejtim të kundërt. Në qoftë se edhe shpejtësia edhe ngarkesa janë përmbys atëherë drejtimi i forcës mbetet i njëjtë. Për këtë arsye matja e fushës magnetike nuk dallon kur ngarkesa është positive dhe lëviz djathtat apo kur është negative dhe lëviz majtas (në të dy rastet prodhohet rrymë e njëjtë). Në dorën tjetër, një fushë magnetike e kombinuar më një fushë elektrike mund të dallohen mes tyre, shih Efektin e Sallës më poshtë.

Një mnemonic alternative i dorës së djathtë është rregulla e dorës së majtë e Flemingut.

Ndërlidhja mes H dhe B

Formulat e nxjerra më lart për fushën magnetike janë të sakta vetëm kur kemi të bëjmë me rrymë të tërë. Një material magnetik i vendosur brenda një fushe magnetike, megjithëse, gjeneron rrymën e vet të lidhur, e cila mund të jetë sfiduese për tu llogaritur (kjo rrymë e lidhur është për shkak të shumës së harqeve të rrymës me madhësi atomike dhe rrotullimit të grimcave subatomike si elektronte që e përbëjnë materialin). Fusha H e definuar si më sipër ndihmon ta faktorizojmë këtë rrymë të lidhur; për të parë si, ajo ndihmon për ta prezantuar konceptin e magnetizmit fillimisht.

Polarizimi magnetik M

Vektori i fushës se polarizuar magnetike (ang: Magnetization) M paraqet se sa fort është i magnetizuar një regjion i materialit. Është përcaktuar si moment magnetik i dipolit për njësi të vëllimit në atë regjion. Fusha e tillë e një magneti uniform është material constant, i barabartë me momentin magnetik m të magnetit pjesëtuar me vëllimin e tij. Që kur njësia e momentit magnetik në SI është Am2, njësia e M në SI është amper për metër, identik me atë të fushës H.

Fusha M e një regjioni tregon në drejtim të momentit mesatar magnetik të dipolit në atë regjion. Vijat e fushës M, kështu, fillojnë afër polit jugor dhe përfundojnë afër polit verior (M nuk ekziston jashtë magnetit).

Në modelin e harqeve aperiane, M është për shkak të kombinimit të shumë harqeve të imëta amperiane për të krijuar një rrymë rezultuese të quajtur rrymë e lidhur. Kjo rrymë e lidhur, atëherë, është burim i fushës magnetike B për shkak të magnetit. Duke përkufizuar dipolin magnetik, fusha M ndjek të njëjtin ligj të Amperit:

\oint \mathbf {M} \cdot d{\boldsymbol {\ell }}=I_{\mathrm {b} },

ku integrali është linjor mbi një konturë të mbyllur dhe Ib është ‘rryma e lidhur’ e mbërthyer në atë hark.

Në modelin e polit magnetik, M fillon dhe përfund në polet e magnetit. Nëse jepet një regjion, prandaj, ka një net pozitiv “fortësia e polit magnetik” (duke iu referuar polit verior) atëherë ka më shumë vija të fushës M që hyjnë sesa që dalin. Matematikisht kjo është ekuivalente

\oint _{S}\mu _{0}\mathbf {M} \cdot \mathrm {d} \mathbf {A} =-q_{M}

,

ku integrali është i mbyllur në një sipërfaqe S dhe qM është “ngarkesë magnetike” (në njësi të fluksit magnetik) e mbërthyer nga S (sipërfaqja e mbyllur e zotëron krejtësisht një regjion pa vrima që nuk i lë vijat e fushës të ikin). Shenjat negative ndodhin sepse fusha M lëvizë nga jugu në very.

Fusha H dhe materialet magnetike

Fusha H është e përkufizuar si:

\mathbf {H} \ \equiv \ {\frac {\mathbf {B} }{\mu _{0}}}-\mathbf {M} ,

(përcaktimi i H-së në sistemin SI)

Me këtë përkufizim, Ligji i Amperit merr formën:

\oint \mathbf {H} \cdot d{\boldsymbol {\ell }}=\oint ({\frac {\mathbf {B} }{\mu _{0}}}-\mathbf {M} )\cdot d{\boldsymbol {\ell }}=I_{\mathrm {tot} }-I_{\mathrm {b} }=I_{\mathrm {f} },

ku If paraqet “rrymën e lirë” e mbërthyer nga harku ashtu që integrali linjor i H-së nuk varet i tëri nga rryma e lidhur.^[4] Për ekuivalentin diferencial të këtij ekuacioni, shih ekuacionet e Maksuellit. Ligji i Amperit udhëhiqet nga kushtet kufitare

(\mathbf {H_{1}^{\parallel }} -\mathbf {H_{2}^{\parallel }} )=\mathbf {K} _{\text{f}}\times {\hat {\mathbf {n} }},

ku Kf është densiteti i sipërfaqës së rrymës së lirë dhe vektori normal tregon në drejtim nga mjedisi 2 në mjedisin 1.

Ngjashëm, integrali syprinor i H-së mbi secilën sipërfaqe të mbyllur është i pavarur nga rrymat e lira dhe prek jashtë “ngarkesës magnetike” përbrenda asaj sipërfaqeje të mbyllur:

\oint _{S}\mu _{0}\mathbf {H} \cdot \mathrm {d} \mathbf {A} =\oint _{S}(\mathbf {B} -\mu _{0}\mathbf {M} )\cdot \mathrm {d} \mathbf {A} =(0-(-q_{M}))=q_{M},

e cila nuk varet nga rrymat e lira. Fusha H, prandaj, mund të ndahet në dy pjesë të pavarura:

\mathbf {H} =\mathbf {H} _{0}+\mathbf {H} _{d},\,

ku H0 është e aplikuar në fushën magnetike për shkak të rrymave të lira dhe Hd është fusha e kundërt M për shkak të rrymave të lidhura.

Fusha magnetike H, prandaj, ri-fakturon rrymën e lidhur në terma të “rrymës magnetike”. Harqet e vijave të fushës H vetëm përreth “rrymës së lirë” dhe, ndryshe nga fusha magnetike B, fillojnë dhe mbarojnë afër poleve magnetike.

Referime

Hans Christian Ørsted, Der Geist in der Natur, 1854

Web

Libra

Carl H. Durney; Curtis C. Johnson (1969). Introduction to modern electromagnetics. McGraw-Hill. ISBN 0-07-018388-0. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

Rao, Nannapaneni N. (1994). Elements of engineering electromagnetics (4th ed.). Prentice Hall. ISBN 0-13-948746-8. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

Jackson, John D. (1999). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

Furlani, Edward P. (2001). Permanent Magnet and Electromechanical Devices: Materials, Analysis and Applications. Academic Press Series in Electromagnetism. ISBN 0-12-269951-3. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

Shënime

^ Purcell, E. (2011). Electricity and Magnetism (bot. 2nd). Cambridge University Press. fq. 173–4. ISBN 1107013607. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
^ "International system of units (SI)". NIST reference on constants, units, and uncertainty. National Institute of Standards and Technology. Marrë më 9 maj 2012. {{cite web}}: Mungon ose është bosh parametri |language= (Ndihmë!)
^ Deissler, R.J. (2008). "Dipole in a magnetic field, work, and quantum spin" (PDF). Physical Review E. 77 (3, pt 2): 036609. Bibcode:2008PhRvE..77c6609D. doi:10.1103/PhysRevE.77.036609. PMID 18517545. Arkivuar nga origjinali (PDF) më 21 korrik 2011. Marrë më 3 prill 2015. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
^ John Clarke Slater, Nathaniel Herman Frank (1969). Electromagnetism (bot. first published in 1947). Courier Dover Publications. fq. 69. ISBN 0-486-62263-0. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

Lidhje te jashtme

Informacion

Crowell, B., "Electromagnetism Arkivuar 3 qershor 2011 tek Wayback Machine".

Nave, R., "Magnetic Field". HyperPhysics.

"Magnetism", The Magnetic Field. theory.uwinnipeg.ca.

Hoadley, Rick, "What do magnetic fields look like Arkivuar 19 shkurt 2011 tek Wayback Machine?" 17 July 2005.

Densiteti i fushës

Jiles, David (1994). Introduction to Electronic Properties of Materials (1st ed.). Springer. ISBN 0-412-49580-5.

Fusha magnetike rrotulluese

"Rotating magnetic fields". Integrated Publishing.

"Introduction to Generators and Motors", rotating magnetic field Arkivuar 7 mars 2005 tek Wayback Machine. Integrated Publishing.

"Induction Motor-Rotating Fields Arkivuar 29 shtator 2005 tek Wayback Machine".

Diagrame

McCulloch, Malcolm,"A2: Electrical Power and Machines", Rotating magnetic field. eng.ox.ac.uk.

"AC Motor Theory" Figure 2 Rotating Magnetic Field Arkivuar 24 gusht 2005 tek Wayback Machine. Integrated Publishing.

Artikuj Revistash

Yaakov Kraftmakher, "Two experiments with rotating magnetic field". 2001 Eur. J. Phys. 22 477-482.

Bogdan Mielnik and David J. Fernández C., "An electron trapped in a rotating magnetic field". Journal of Mathematical Physics, February 1989, Volume 30, Issue 2, pp. 537-549.

Sonia Melle, Miguel A. Rubio and Gerald G. Fuller "Structure and dynamics of magnetorheological fluids in rotating magnetic fields". Phys. Rev. E 61, 4111 – 4117 (2000).

[purcell-1] Purcell, E. (2011). Electricity and Magnetism (bot. 2nd). Cambridge University Press. fq. 173–4. ISBN 1107013607. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[2] "International system of units (SI)". NIST reference on constants, units, and uncertainty. National Institute of Standards and Technology. Marrë më 9 maj 2012. {{cite web}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[Deissler-3] Deissler, R.J. (2008). "Dipole in a magnetic field, work, and quantum spin" (PDF). Physical Review E. 77 (3, pt 2): 036609. Bibcode:2008PhRvE..77c6609D. doi:10.1103/PhysRevE.77.036609. PMID 18517545. Arkivuar nga origjinali (PDF) më 21 korrik 2011. Marrë më 3 prill 2015. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[4] John Clarke Slater, Nathaniel Herman Frank (1969). Electromagnetism (bot. first published in 1947). Courier Dover Publications. fq. 69. ISBN 0-486-62263-0. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[1]

[2]

[3]

[4]