Polinom i Lagranzhit

Në analizën numerike, polinomi interpolues i Lagranzhit është polinomi unik i shkallës më të ulët që interpolon një bashkësi të caktuar të dhënash.

Ky imazh tregon, për katër pika ( ( − 9, 5), ( − 4, 2), ( − 1, − 2), (7, 9) ), polinomi i interpolimit (kubik) $L(x)$ (i ndërprerë, i zi), i cili është shuma e polinomeve të bazës të shkallëzuara y ₀ ℓ ₀ ( x ), y ₁ ℓ ₁ ( x ), y ₂ ℓ ₂ ( x ) dhe y ₃ ℓ ₃ ( x ) . Polinomi i interpolimit kalon nëpër të katër pikat e kontrollit, dhe çdo polinom i bazës i shkallëzuar kalon nëpër pikën e tij përkatëse të kontrollit dhe është 0 ku x përkon me tre pikat e tjera të kontrollit.

Jepet një bashkësi të dhënash në formën e çifteve koordinative $(x_{j},y_{j})$ me $0\leq j\leq k,$ të $x_{j}$ quhen nyje dhe $y_{j}$ quhen vlera . Polinomi i Lagranzhit $L(x)$ ka shkallë ${\textstyle \leq k}$ dhe merr çdo vlerë në nyjen përkatëse, $L(x_{j})=y_{j}.$

Edhe pse i emërtuar sipas Jozef-Luis Lagranzhit, i cili e botoi atë në 1795, metoda u zbulua për herë të parë në 1779 nga Edward Waring . Është gjithashtu një pasojë e lehtë e një formule të botuar në 1783 nga Leonhard Euleri .

Përdorimet e polinomeve të Lagranzhit përfshijnë metodën Newton-Cotes të integrimit numerik, skemën e ndarjes së fshehtë të Shamirit në kriptografi dhe korrigjimin e gabimit Reed-Solomon në teorinë e kodimit .

Për nyjet e barazlarguara, interpolimi i Lagranzhit është i ndjeshëm ndaj dukurisë së luhatjes së madhe të Runges .

Përkufizimi

Duke pasur parasysh një bashkësi prej ${\textstyle k+1}$ nyjesh $\{x_{0},x_{1},\ldots ,x_{k}\}$, të cilat duhet të jenë të gjitha të veçanta, $x_{j}\neq x_{m}$ për indekset $j\neq m$, baza e Lagranzhit për polinomet e shkallës ${\textstyle \leq k}$ për këto nyje është bashkësia e polinomeve ${\textstyle \{\ell _{0}(x),\ell _{1}(x),\ldots ,\ell _{k}(x)\}}$ secila e shkallës ${\textstyle k}$ të cilat marrin vlera ${\textstyle \ell _{j}(x_{m})=0}$ nëse ${\textstyle m\neq j}$ dhe ${\textstyle \ell _{j}(x_{j})=1}$ . Duke përdorur deltën e Kronecker, kjo mund të shkruhet ${\textstyle \ell _{j}(x_{m})=\delta _{jm}.}$ Çdo polinom bazë mund të përshkruhet në mënyrë të shkoqur nga produkti:$${\begin{aligned}\ell _{j}(x)&={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}}\\[10mu]&=\prod _{\begin{smallmatrix}0\leq m\leq k\\m\neq j\end{smallmatrix}}{\frac {x-x_{m}}{x_{j}-x_{m}}}.\end{aligned}}$$Vini re se numëruesi ${\textstyle \prod _{m\neq j}(x-x_{m})}$ ka ${\textstyle k}$ rrënjë në nyjet ${\textstyle \{x_{m}\}_{m\neq j}}$ ndërsa emëruesi ${\textstyle \prod _{m\neq j}(x_{j}-x_{m})}$ shkallëzon polinomin që rezulton në mënyrë që ${\textstyle \ell _{j}(x_{j})=1.}$

Polinomi interpolues i Lagranzhit për ato nyje përmes vlerave përkatëse $\{y_{0},y_{1},\ldots ,y_{k}\}$ është kombinimi linear:$$L(x)=\sum _{j=0}^{k}y_{j}\ell _{j}(x).$$Çdo polinom i bazës ka shkallë ${\textstyle k}$, pra shuma ${\textstyle L(x)}$ ka shkallë ${\textstyle \leq k}$, dhe interpolon të dhënat sepse ${\textstyle L(x_{m})=\sum _{j=0}^{k}y_{j}\ell _{j}(x_{m})=\sum _{j=0}^{k}y_{j}\delta _{mj}=y_{m}.}$

Polinomi interpolues është unik.

Një këndvështrim nga algjebra lineare

Zgjidhja e një problemi interpolimi çon në një problem të algjebrës lineare që arrin në të anasjelltën e një matrice. Duke përdorur një bazë monomiale standarde për polinomin tonë të interpolimit ${\textstyle L(x)=\sum _{j=0}^{k}x^{j}m_{j}}$, duhet të marrim të anasjelltën e matricëns Vandermonde $(x_{i})^{j}$ te zgjidhesh $L(x_{i})=y_{i}$ për koeficientët $m_{j}$ të $L(x)$ . Duke zgjedhur një bazë më të mirë, bazën e Lagranzhit, ${\textstyle L(x)=\sum _{j=0}^{k}l_{j}(x)y_{j}}$, ne thjesht marrim matricën identitet, $\delta _{ij}$, e cila është e anasjellta e saj: baza e Lagranzhit inverton automatikisht analogun e matricës Vandermonde.

Shembull

Ne dëshirojmë të interpolojmë $f(x)=x^{2}$ mbi segmentin $1\leq x\leq 3$ në tre nyjet $\{1,\,2,\,3\}$:

${\begin{aligned}x_{0}&=1,&&&y_{0}=f(x_{0})&=1,\\[3mu]x_{1}&=2,&&&y_{1}=f(x_{1})&=4,\\[3mu]x_{2}&=3,&&&y_{2}=f(x_{2})&=9.\end{aligned}}$

Polinomi i nyjës, $\ell$ , është

$\ell (x)=(x-1)(x-2)(x-3)=x^{3}-6x^{2}+11x-6.$

Peshat baricentrike janë

${\begin{aligned}w_{0}&=(1-2)^{-1}(1-3)^{-1}={\tfrac {1}{2}},\\[3mu]w_{1}&=(2-1)^{-1}(2-3)^{-1}=-1,\\[3mu]w_{2}&=(3-1)^{-1}(3-2)^{-1}={\tfrac {1}{2}}.\end{aligned}}$

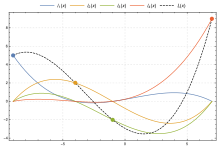
Polinomet e bazës së Lagranzhit janë

${\begin{aligned}\ell _{0}(x)&={\frac {x-2}{1-2}}\cdot {\frac {x-3}{1-3}}={\tfrac {1}{2}}x^{2}-{\tfrac {5}{2}}x+3,\\[5mu]\ell _{1}(x)&={\frac {x-1}{2-1}}\cdot {\frac {x-3}{2-3}}=-x^{2}+4x-3,\\[5mu]\ell _{2}(x)&={\frac {x-1}{3-1}}\cdot {\frac {x-2}{3-2}}={\tfrac {1}{2}}x^{2}-{\tfrac {3}{2}}x+1.\end{aligned}}$

Polinomi interpolues i Lagranzhit është:

${\begin{aligned}L(x)&=1\cdot {\frac {x-2}{1-2}}\cdot {\frac {x-3}{1-3}}+4\cdot {\frac {x-1}{2-1}}\cdot {\frac {x-3}{2-3}}+9\cdot {\frac {x-1}{3-1}}\cdot {\frac {x-2}{3-2}}\\[6mu]&=x^{2}.\end{aligned}}$

Në formën (e dytë) baricentrike,

$L(x)={\frac {\displaystyle \sum _{j=0}^{2}{\frac {w_{j}}{x-x_{j}}}y_{j}}{\displaystyle \sum _{j=0}^{2}{\frac {w_{j}}{x-x_{j}}}}}={\frac {\displaystyle {\frac {\tfrac {1}{2}}{x-1}}+{\frac {-4}{x-2}}+{\frac {\tfrac {9}{2}}{x-3}}}{\displaystyle {\frac {\tfrac {1}{2}}{x-1}}+{\frac {-1}{x-2}}+{\frac {\tfrac {1}{2}}{x-3}}}}.$

Shiko gjithashtu

• Algoritmi i Nevilit
• Forma e Njutonit të polinomit të interpolimit
• Polinomi Bernshtajn
• Teorema e Karlsonit
• Konstantja e Lebegut (interpolimi)
• Sistemi Chebfun
• Tabela e serive Njutoniane
• Kovarianti i Frobeniusit
• Formula e Silvesterit
• Koeficienti i diferencës së fundme
• Interpolimi i Hermitit