Funksioni sigmoid

Një funksion sigmoid është një funksion matematikor që ka një kurbë karakteristike në formë "S" ose kurbë sigmoide .

Kurba logjistike

Vizatimi i funksionit të gabimit

Një shembull i zakonshëm i një funksioni sigmoid është funksioni logjistik i paraqitur në figurën e parë dhe i përcaktuar nga formula:

$\sigma (x)={\frac {1}{1+e^{-x}}}={\frac {e^{x}}{1+e^{x}}}=1-\sigma (-x).$

Një shumëllojshmëri e gjerë funksionesh sigmoide, duke përfshirë funksionet tangjente logjistike dhe hiperbolike, janë përdorur si funksione aktivizimi të neuroneve artificalë. Lakoret sigmoide janë gjithashtu të zakonshme në statistikë si funksione mbledhëse të shpërndarjes (të cilat shkojnë nga 0 në 1), të tilla si integralet e densitetit logjistik, densitetit normal dhe funksioneve të dëndësisë së probabilitetit t Studentit . Funksioni logjistik sigmoid është i kthyeshëm dhe i anasjellti i tij është funksioni logit .

E ç'është funksioni sigmoid?

Një funksion sigmoid është një funksion real i kufizuar, i diferencueshëm, i përcaktuar për të gjitha vlerat e hyrjes reale dhe ka një derivat jo negativ në secilën pikë dhe vetëm një pikë infleksioni . Një "funksion" sigmoid dhe një "lakore" sigmoide i referohen të njëjtit objekt.

Vetitë

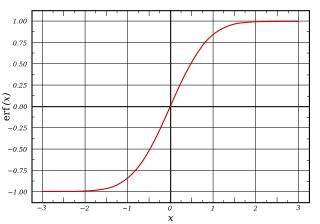
Në përgjithësi, një funksion sigmoid është monoton, dhe ka një derivat të parë që është në formë zile . Anasjelltas, integrali i çdo funksioni të vazhdueshëm, jo-negativ, në formë zile (me një maksimum lokal dhe asnjë minimum lokal, përveç rastit të degjeneruar) do të jetë sigmoidal. Kështu, funksionet e shpërndarjes kumulative për shumë shpërndarje të zakonshme të probabilitetit janë sigmoidale. Një shembull i tillë është funksioni i gabimit, i cili lidhet me funksionin e shpërndarjes kumulative të një shpërndarjeje normale ; një tjetër është funksioni arctan, i cili lidhet me funksionin e shpërndarjes kumulative të një shpërndarjeje Cauchy .

Një funksion sigmoid kufizohet nga një palë asimptota horizontale kur $x\rightarrow \pm \infty$ .

Shembuj

Krahasuar disa funksione sigmoide. Në vizatim të gjitha funksionet janë normalizuar në atë mënyrë që pjerrësia e tyre në origjinë të jetë 1.

• Funksioni logjistik $$f(x)={\frac {1}{1+e^{-x}}}$$
• Tangjentja hiperbolike (versioni i zhvendosur dhe i shkallëzuar i funksionit logjistik, më sipër) $$f(x)=\tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$$
• Funksioni arktangent $$f(x)=\arctan x$$
• Funksioni Gudermannian $$f(x)=\operatorname {gd} (x)=\int _{0}^{x}{\frac {dt}{\cosh t}}=2\arctan \left(\tanh \left({\frac {x}{2}}\right)\right)$$
• Funksioni i gabimit $$f(x)=\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt$$
• Funksioni logjistik i përgjithësuar $$f(x)=\left(1+e^{-x}\right)^{-\alpha },\quad \alpha >0$$
• Funksioni haplëmuar $$f(x)={\begin{cases}{\displaystyle \left(\int _{0}^{1}\left(1-u^{2}\right)^{N}du\right)^{-1}\int _{0}^{x}\left(1-u^{2}\right)^{N}\ du},&|x|\leq 1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\quad N\in \mathbb {Z} \geq 1$$
• Disa funksione algjebrike, për shembull $$f(x)={\frac {x}{\sqrt {1+x^{2}}}}$$
• dhe në një formë më të përgjithshme $$f(x)={\frac {x}{\left(1+|x|^{k}\right)^{1/k}}}$$
• Deri në ndërrime dhe shkallëzime, shumë sigmoide janë raste të veçanta të $$f(x)=\varphi (\varphi (x,\beta ),\alpha ),$$
• Interpolimi i qetë i normalizuar në (-1,1) dhe $n$ është pjerrësia në zero:
• $${\begin{aligned}f(x)&={\begin{cases}{\displaystyle {\frac {2}{1+e^{-2n{\frac {x}{1-x^{2}}}}}}-1},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\\&={\begin{cases}{\displaystyle \tanh \left(n{\frac {x}{1-x^{2}}}\right)},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\end{aligned}}$$

Zbatimet

Shumë procese natyrore, si ato të kurbave komplekse të të mësuarit, shfaqin një përparim të vogël në fillim që përshpejton dhe i afrohet një kulmi me kalimin e kohës. Kur mungon një model specifik matematikor, shpesh përdoret një funksion sigmoid.

Modeli van Genuchten-Gupta bazohet në një kurbë S të përmbysur dhe aplikohet në përgjigjen e rendimentit të bimëve ndaj kripësisë së tokës .

Në rrjetet nervore artificiale, nganjëherë në vend të tyre përdoren funksione jo të lëmuara për efikasitet; këto njihen si sigmoide të forta .

Në përpunimin e sinjalit audio, funksionet sigmoide përdoren si funksione të transferimit të formës së valës për të imituar tingullin e prerjes së qarkut analog .

Në biokimi dhe farmakologji, ekuacionet Hill dhe Hill-Langmuir janë funksione sigmoide.

Në grafikën kompjuterike dhe renderimin në kohë reale, disa nga funksionet sigmoide përdoren për të përzier ngjyrat ose gjeometrinë midis dy vlerave, pa probleme dhe pa shtresa ose ndërprerje të dukshme.