Shpërndarja e arksinusit

Në teorinë e probabilitetit, shpërndarja e arksinusit është shpërndarja e probabilitetit, funksioni mbledhës i shpërndarjes të së cilës përfshin arksinusin dhe rrënjën katrore :

Arksinus

Probability density function Funksioni i dendësisë së probabilitetit
Cumulative distribution function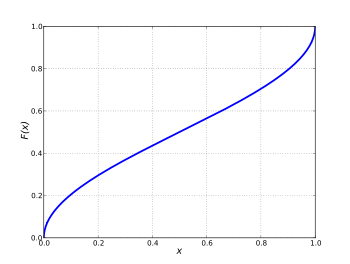
Parametrat	asnjë
Mbështetës	$x\in [0,1]$
FDGJ	$f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}$
FGSH	$F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)$
Vlera e pritur	${\frac {1}{2}}$
Mediana	${\frac {1}{2}}$
Moda	$x\in \{0,1\}$
Varianca	${\tfrac {1}{8}}$
Shtrirja	$0$
Kurtoza e tepërt	$-{\tfrac {3}{2}}$
Entropia	$\ln {\tfrac {\pi }{4}}$
FGJM	$1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {2r+1}{2r+2}}\right){\frac {t^{k}}{k!}}$
FK	${}_{1}F_{1}({\tfrac {1}{2}};1;i\,t)\$

$F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)={\frac {\arcsin(2x-1)}{\pi }}+{\frac {1}{2}}$

për 0 ≤ x ≤ 1, dhe funksioni i densitetit të probabilitetit të të cilit është

$f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}$

në $(0,1)$. Shpërndarja standarde e arksinusit është një rast i veçantë i shpërndarjes beta me $\alpha =\beta =1/2$. Kjo është, nëse $X$ është një ndryshore e rastit me ligj arksinusi, atëherë $X\sim {\rm {Beta}}{\bigl (}{\tfrac {1}{2}},{\tfrac {1}{2}}{\bigr )}$. Sipas shtrirjes, shpërndarja e arksinusit është një rast i veçantë i shpërndarjes së tipit I të Pearson .

Përgjithësim

Bashkësia e përcaktimi të arksinusit të kufizuar

Parametrat	$-\infty <a<b<\infty \,$
Mbështetës	$x\in [a,b]$
	$f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}$
FGSH	$F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)$
Vlera e pritur	${\frac {a+b}{2}}$
Mediana	${\frac {a+b}{2}}$
Moda	$x\in {a,b}$
	${\tfrac {1}{8}}(b-a)^{2}$
Shtrirja	$0$
Kurtoza e tepërt	$-{\tfrac {3}{2}}$

BP e kufizuar arbitrarisht

Shpërndarja mund të zgjerohet për të përfshirë çdo bashkësi përcaktimi të kufizuar nga $a\leq x\leq b$ me një transformim të thjeshtë

$F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)$

për një $a\leq x\leq b$, dhe funksioni i densitetit probabilitar të të cilit është

$f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}$

në $(a,b)$.

Faktori i formës

Shpërndarja standarde e përgjithësuar e arksinusit në intervalin $(0,1)$ me funksion të densitetit të probabilitetit

$f(x;\alpha )={\frac {\sin \pi \alpha }{\pi }}x^{-\alpha }(1-x)^{\alpha -1}$

është gjithashtu një rast i veçantë i shpërndarjes beta me parametra ${\rm {Beta}}(1-\alpha ,\alpha )$ .

Vetitë

• Shpërndarja e arksinusit është e mbyllur nën translatim dhe shkallëzim me një faktor pozitiv
  • Nëse $X\sim {\rm {Arcsine}}(a,b)\ {\text{atëherë }}kX+c\sim {\rm {Arcsine}}(ak+c,bk+c)$
• Katrori i një shpërndarjeje arksinusi mbi $(-1,1)$ ka shpërndarje arksine mbi $(0,1)$
  • Nëse $X\sim {\rm {Arcsine}}(-1,1)\ {\text{atëherë }}X^{2}\sim {\rm {Arcsine}}(0,1)$
• Koordinatat e pikave të zgjedhura në mënyrë të njëtrajtshme në një rreth me rreze $r$ me qendër në origjinë $(0,0)$, kanë një shpërndarje ${\rm {Arcsine}}(-r,r)$
  • Për shembull, nëse zgjedhim një pikë në mënyrë të njëtrajtshme në perimetër, $U\sim {\rm {Uniform}}(0,2\pi r)$, marrim shpërndarjen e koordinatave x të pikës është $r\cdot \cos(U)\sim {\rm {Arcsine}}(-r,r)$, dhe shpërndarja e koordinatave y të saj është ${\textstyle r\cdot \sin(U)\sim {\rm {Arcsine}}(-r,r)}$

Shpërndarjet e ndërlidhura

• Nëse $U$ dhe $V$ janë ndryshore rasti iid uniforme $(-\pi ,\pi )$, atëherë $\sin(U)$, $\sin(2U)$, $-\cos(2U)$, $\sin(U+V)$ dhe $\sin(U-V)$ të gjithë kanë një shpërndarje ${\rm {Arcsine}}(-1,1)$.
• Nëse $X$ është shpërndarja e përgjithësuar e arksinusit me parametrin e formës $\alpha$ mbështetur në intervalin e fundëm $[a,b]$ atëherë ${\frac {X-a}{b-a}}\sim {\rm {Beta}}(1-\alpha ,\alpha )\$
• Nëse $X\sim \operatorname {Cauchy} (0,1)$ atëherë ${\tfrac {1}{1+X^{2}}}$ ndjek një shpërndarje standarde arksinusi.

Aplikacion

Shpërndarja e arksinusit gjen zbatim në formimin e rrezeve dhe sintezën e modelit. Është gjithashtu dendësia klasike e probabilitetit për oshilatorin e thjeshtë harmonik .