Funksioni mbledhës i shpërndarjes

Në teorinë dhe statistikat e probabilitetit, funksioni mbledhës i shpërndarjes ( FMSH) i një ndryshoreje të rastit me vlera reale $X$ , ose thjesht funksioni i shpërndarjes së $X$ , vlerësuar në $x$ , është probabiliteti që $X$ do të marrë një vlerë më të vogël ose të barabartë me $x$ . ^[1]

Çdo shpërndarje probabiliteti e mbështetur në numrat realë, diskrete ose "të përziera" si dhe të vazhdueshme, identifikohet në mënyrë unike nga një funksion rritës monoton i vazhdueshëm djathtas (një funksion càdlàg ) $F\colon \mathbb {R} \rightarrow [0,1]$ që kënaq $\lim _{x\rightarrow -\infty }F(x)=0$ dhe $\lim _{x\rightarrow \infty }F(x)=1$ .

E ç'është FMSH?

Funksioni mbledhës i shpërndarjes së një ndryshoreje të rastit me vlera reale $X$ është funksioni i dhënë nga ^[2] ^{:p. 77}Stampa:Equation box 1 $F_{X}(x)=\operatorname {P} (X\leq x)$

ku ana e djathtë paraqet probabilitetin që ndryshorja e rastit $X$ merr një vlerë më të vogël ose të barabartë me $x$ .

Probabiliteti që $X$ shtrihet në intervalin gjysmë të mbyllur $(a,b]$ , ku $a<b$ , pra është ^[2] ^{:p. 84}

$\operatorname {P} (a<X\leq b)=F_{X}(b)-F_{X}(a)$

Në përkufizimin e mësipërm, shenja "më pak se ose e barabartë me", "≤", është një konventë, jo një përdorim universal (p.sh. literatura hungareze përdor "<"), por dallimi është i rëndësishëm për shpërndarjet diskrete. Përdorimi i duhur i tabelave të shpërndarjeve binomiale dhe Poisson varet nga kjo konventë. Për më tepër, formula të rëndësishme si formula e përmbysjes së Paul Lévy -t për funksionin karakteristik gjithashtu mbështeten në formulimin "më pak ose të barabartë".

Funksioni i dendësisë së probabilitetit të një ndryshoreje të rastit të vazhdueshme mund të përcaktohet nga funksioni i shpërndarjes mbledhëse duke diferencuar ^[3] duke përdorur Teoremën Themelore të Kalkulusit ; dmth i dhënë $F(x)$ , $f(x)={\frac {dF(x)}{dx}}$ përderisa ekziston derivati.

FMSH e një ndryshoreje të rastit të vazhdueshme $X$ mund të shprehet si integral i funksionit të dendësisë së probabilitetit të tij $f_{X}$ si më poshtë: ^[2] ^{:p. 86} $F_{X}(x)=\int _{-\infty }^{x}f_{X}(t)\,dt.$

Vetitë

Nga lart poshtë, funksioni i shpërndarjes mbledhëse i një shpërndarjeje diskrete të probabilitetit, shpërndarjes së vazhdueshme të probabilitetit dhe një shpërndarje që ka një pjesë të vazhdueshme dhe një pjesë diskrete.

Shembull i një funksioni shpërndarjeje mbledhëse me një grup ndërprerjesh të pafundme të numërueshme.

Çdo funksion mbledhës i shpërndarjes $F_{X}$ është jozbritës ^[2] ^{:p. 78}dhe i vazhdueshëm nga e djathta, ^[2] ^{:p. 79}gjë që e bën atë një funksion càdlàg . Për më tepër, $\lim _{x\to -\infty }F_{X}(x)=0,\quad \lim _{x\to +\infty }F_{X}(x)=1.$ Nëse $X$ është një ndryshore e rastit e pastër diskrete, atëherë ajo arrin vlera $x_{1},x_{2},\ldots$ me probabilitet $p_{i}=p(x_{i})$ , dhe CDF e $X$ do të jetë i ndërprerë në pika $x_{i}$ : $F_{X}(x)=\operatorname {P} (X\leq x)=\sum _{x_{i}\leq x}\operatorname {P} (X=x_{i})=\sum _{x_{i}\leq x}p(x_{i}).$ Nëse FMSH $F_{X}$ të një ndryshoreje të rastit me vlera reale $X$ është e vazhdueshme, atëherë $X$ është një ndryshore e rastit e vazhdueshme ; nëse për më tepër $F_{X}$ është absolutisht i vazhdueshëm, atëherë ekziston një funksion i integrueshëm sipas Lebesgue $f_{X}(x)$ i tillë që $F_{X}(b)-F_{X}(a)=\operatorname {P} (a<X\leq b)=\int _{a}^{b}f_{X}(x)\,dx$ për të gjithë numrat realë $a$ dhe $b$ . Funksioni $f_{X}$ është e barabartë me derivatin e $F_{X}$ pothuajse kudo, dhe quhet funksioni i dendësisë së probabilitetit të shpërndarjes së $X$ .

Plot FMSH me dy drejtkëndësha të kuq, që ilustron

x(1-F_{X}(x))\leq \int _{x}^{\infty }tdF_{X}(t)

dhe

xF_{X}(-x)\leq \int _{-\infty }^{-x}(-t)dF_{X}(t)

.

Shembuj

Si shembull, supozoni $X$ shpërndahet në mënyrë uniforme në intervalin e njësisë $[0,1]$ .

Pastaj FMSH e $X$ jepet nga $F_{X}(x)={\begin{cases}0&:\ x<0\\x&:\ 0\leq x\leq 1\\1&:\ x>1\end{cases}}$ Supozoni se në vend të kësaj $X$ merr vetëm vlerat diskrete 0 dhe 1, me probabilitet të barabartë.

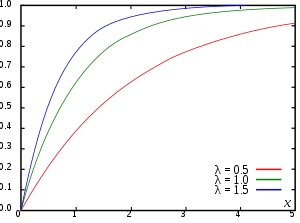
Pastaj FMSH e $X$ jepet nga $F_{X}(x)={\begin{cases}0&:\ x<0\\1/2&:\ 0\leq x<1\\1&:\ x\geq 1\end{cases}}$ Supozoni $X$ është i shpërndarë në mënyrë eksponenciale . Pastaj FMSH e $X$ jepet nga $F_{X}(x;\lambda )={\begin{cases}1-e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$ Këtu λ > 0 është parametri i shpërndarjes, i quajtur shpesh parametri i shpejtësisë.

Supozoni $X$ shpërndahet normalisht . Pastaj FMSH e $X$ jepet nga $F(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{x}\exp \left(-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}\right)\,dt.$ Këtu është parametri $\mu$ është mesatarja ose pritshmëria e shpërndarjes; dhe $\sigma$ është devijimi standard i saj.

Supozoni $X$ është i shpërndarë binomialisht . Pastaj FMSH e $X$ jepet nga $F(k;n,p)=\Pr(X\leq k)=\sum _{i=0}^{\lfloor k\rfloor }{n \choose i}p^{i}(1-p)^{n-i}$

Funksioni i anasjelltë (funksioni kuantile)

Nëse FMSH F është rreptësisht rritës dhe i vazhdueshëm atëherë $F^{-1}(p),p\in [0,1],$ është numri real unik $x$ sikurse $F(x)=p$ . Kjo përcakton funksionin e shpërndarjes së kundërt ose funksionin kuantile .

Disa shpërndarje nuk kanë një të anasjelltë unik (për shembull nëse $f_{X}(x)=0$ per te gjithe $a<x<b$ , duke bërë që $F_{X}$ të jetë konstante). Në këtë rast, mund të përdoret funksioni i përgjithësuar i shpërndarjes së anasjelltë, i cili përkufizohet si

F^{-1}(p)=\inf\{x\in \mathbb {R} :F(x)\geq p\},\quad \forall p\in [0,1].

Shembulli 1: Mediana është $F^{-1}(0.5)$ .
Shembulli 2: Vendos $\tau =F^{-1}(0.95)$ . Kështu thërritet $\tau$ përqindja e 95-të.

Disa veti të dobishme të fmsh-së së anasjelltë (të cilat ruhen gjithashtu në përkufizimin e funksionit të shpërndarjes së përgjithësuar të anasjelltë) janë:

$F^{-1}$ është jozbritës
$F^{-1}(F(x))\leq x$
$F(F^{-1}(p))\geq p$
$F^{-1}(p)\leq x$ atëherë dhe vetëm atëherë nëse $p\leq F(x)$
Nëse $Y$ ka një shpërndarje $U[0,1]$ pastaj $F^{-1}(Y)$ shpërndahet si $F$ . Kjo përdoret në gjenerimin e numrave të rastit duke përdorur metodën e kampionimit të transformimit të kundërt .
Nëse $\{X_{\alpha }\}$ është një koleksion i pavarur $F$ -variabla të rastit të shpërndara të përcaktuara në të njëjtën hapësirë popullimi, atëherë ekzistojnë variabla të rastësishme $Y_{\alpha }$ sikurse $Y_{\alpha }$ shpërndahet si $U[0,1]$ dhe $F^{-1}(Y_{\alpha })=X_{\alpha }$ me probabilitet 1 për të gjithë $\alpha$ . ^{[ citim i nevojshëm ]}

Rasti me shumë ndryshore

Përkufizimi për dy ndryshore të rastit

Kur kemi të bëjmë njëkohësisht me më shumë se një ndryshore të rastit , funksioni i përbashkët mbledhës i shpërndarjes gjithashtu mund të përcaktohet. Për shembull, për një palë ndryshoresh të rastit $X,Y$ , CDF e përbashkët $F_{XY}$ jepet nga ^[2] ^{:p. 89}Stampa:Equation box 1 $F_{X,Y}(x,y)=\operatorname {P} (X\leq x,Y\leq y)$

ku ana e djathtë paraqet probabilitetin që ndryshorja e rastit $X$ merr një vlerë më të vogël ose të barabartë me $x$ dhe atë $Y$ merr një vlerë më të vogël ose të barabartë me $y$ .

Shembull i funksionit të përbashkët të shpërndarjes mbledhëse:

Për dy ndryshore të vazhduara $X$ dhe $Y$ : $\Pr(a<X<b{\text{ and }}c<Y<d)=\int _{a}^{b}\int _{c}^{d}f(x,y)\,dy\,dx;$ Për dy ndryshore të rastësishme diskrete, është e dobishme të gjenerohet një tabelë e probabiliteteve dhe të adresohet probabiliteti mbledhës për çdo shtrirje potenciale të $X$ dhe $Y$ , dhe këtu është shembulli: ^[4]

duke pasur parasysh funksionin e masës së probabilitetit të përbashkët në formë tabelare, përcaktoni funksionin e shpërndarjes mbledhëse të përbashkët.

	Y = 2	Y = 4	Y = 6	Y = 8
X = 1	0	0.1	0	0.1
X = 3	0	0	0.2	0
X = 5	0.3	0	0	0.15
X = 7	0	0	0.15	0

Zgjidhje: duke përdorur tabelën e dhënë të probabiliteteve për çdo varg potencial të $X$ dhe $Y$ , funksioni i përbashkët kumulativ i shpërndarjes mund të ndërtohet në formë tabelare:

	Y < 2	2 ≤ Y < 4	4 ≤ Y < 6	6 ≤ Y < 8	Y ≥ 8
X < 1	0	0	0	0	0
1 ≤ X < 3	0	0	0.1	0.1	0.2
3 ≤ X < 5	0	0	0.1	0.3	0.4
5 ≤ X < 7	0	0.3	0.4	0.6	0,85
X ≥ 7	0	0.3	0.4	0.75	1

^ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Mathematics for Machine Learning. Cambridge University Press. fq. 181. ISBN 9781108455145. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
^ ^a ^b ^c ^d ^e ^f Park, Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "KunIlPark" defined multiple times with different content
^ Montgomery, Douglas C.; Runger, George C. (2003). Applied Statistics and Probability for Engineers (PDF). John Wiley & Sons, Inc. fq. 104. ISBN 0-471-20454-4. Arkivuar (PDF) nga origjinali më 2012-07-30. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
^ "Joint Cumulative Distribution Function (CDF)". math.info. Marrë më 2019-12-11. {{cite web}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[1] Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Mathematics for Machine Learning. Cambridge University Press. fq. 181. ISBN 9781108455145. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[KunIlPark-2] ^ ^a ^b ^c ^d ^e ^f Park, Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "KunIlPark" defined multiple times with different content

[3] Montgomery, Douglas C.; Runger, George C. (2003). Applied Statistics and Probability for Engineers (PDF). John Wiley & Sons, Inc. fq. 104. ISBN 0-471-20454-4. Arkivuar (PDF) nga origjinali më 2012-07-30. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[4] "Joint Cumulative Distribution Function (CDF)". math.info. Marrë më 2019-12-11. {{cite web}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[1]

[2]

[3]

[4]