Forca e Lorencit

Në fizikë, forca e Lorencit është një forcë mbi një pikë ngarkese në saje të fushës elektromagnetike. Jepet nga ekuacioni i mëposhtëm ne terma te fushës elektrike dhe asaj magnetike:

Trajektorja e një thërrmije me ngarkese q, nën ndikimin e një fushe magnetike B (e drejtuar në mënyrë perpendikulare jashtë ekranit), për vlera të ndryshme të q-së.

$\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),$

,ku

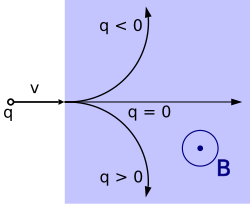
F është forca (në njuton)

E është fusha elektrike (në volt për metër)

B është induksioni i fushes magnetike (në tesla)

q është ngarkesa elektrike e thërrmijës (në kulomb)

v është shpejtësia e çastit të thërrmijës (në metër për sekondë)

l- si vektor qe ka drejtimin e percjellesit, kahun e rrjedhjes së rrymë dhe intensitetin e barabartë me gjatësinë e pëcjellësit.

× është prodhimi vektorial

∇ dhe ∇ × janë gradienti dhe kerli, respektivisht

Ose ne mënyrë ekuivalente kemi këtë ekuacionin e mëposhtëm te dhënë në term për potencialit vektorial dhe për potencialit skalar:

$\mathbf {F} =q(-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\mathbf {v} \times (\nabla \times \mathbf {A} )),$

ku:

A dhe ɸ janë potenciali magnetik vektorial dhe potenciali elektrostatik, respektivisht, të cilat janë te lidhura me E dhe B nga

$\mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}$

$\mathbf {B} =\nabla \times \mathbf {A} .$