Identiteti (matematikë)

Në matematikë, një identitet është një barazi që lidh një shprehje matematikore A me një shprehje tjetër matematikore B, të tilla që A dhe B (të cilat mund të përmbajnë disa ndryshore ) prodhojnë të njëjtën vlerë për të gjitha vlerat e ndryshoreve brenda një diapazoni të caktuar vlefshmërie. Me fjalë të tjera, A = B është një identitet nëse A dhe B përcaktojnë të njëjtat funksione, dhe një identitet është një barazi midis funksioneve që përcaktohen ndryshe. Për shembull, $(a+b)^{2}=a^{2}+2ab+b^{2}$ dhe $\cos ^{2}\theta +\sin ^{2}\theta =1$ janë identitete.

Dëshmi pamore e identitetit të Pitagorës : për çdo kënd $\theta$, pika $(x,y)=(\cos \theta ,\sin \theta )$ shtrihet në rrethin njësi, i cili kënaq ekuacionin $x^{2}+y^{2}=1$ . Kështu, $\cos ^{2}\theta +\sin ^{2}\theta =1$ .

Identitetet nganjëherë tregohen me simbolin e shiritit të trefishtë ≡ në vend të =, shenjë e barazimit .

Identitete të përbashkëta

Identitetet algjebrike

Identitete të caktuara, si p.sh $a+0=a$ dhe $a+(-a)=0$, përbëjnë bazën e algjebrës, ndërsa identitetet e tjera, si p.sh $(a+b)^{2}=a^{2}+2ab+b^{2}$ dhe $a^{2}-b^{2}=(a+b)(a-b)$, mund të jetë të dobishme në thjeshtimin e shprehjeve algjebrike dhe zgjerimin e tyre.

Identitete trigonometrike

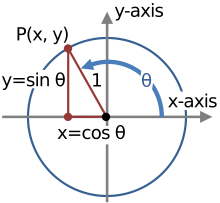
Gjeometrikisht, identitetet trigonometrike janë identitete që përfshijnë funksione të caktuara të një ose më shumë këndeve . Ato dallohen nga identitetet e trekëndëshit, të cilat janë identitete që përfshijnë kënde dhe gjatësi anësore të një trekëndëshi.

One of the most prominent examples of trigonometric identities involves the equation $\sin ^{2}\theta +\cos ^{2}\theta =1,$ which is true for all real values of $\theta$. On the other hand, the equation

$\cos \theta =1$

është e vërtetë vetëm për vlera të caktuara të $\theta$, jo të gjithë. Për shembull, ky ekuacion është i vërtetë kur $\theta =0,$ por false kur $\theta =2$ .

Identitete eksponenciale

Identitetet e mëposhtme vlejnë për të gjithë eksponentët e numrave të plotë, me kusht që baza të jetë jo zero:

${\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\(b^{m})^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}$

Identitete logaritmike

Disa formula të rëndësishme, nganjëherë të quajtura identitete logaritmike ose ligje log, i lidhin logaritmet me njëri-tjetrin:

	Formula	Shembull
prodhimi	$\log _{b}(xy)=\log _{b}(x)+\log _{b}(y)$	$\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5$
herësi	$\log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)$	$\log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4$
fuqia	$\log _{b}(x^{p})=p\log _{b}(x)$	$\log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6$
rrënja	$\log _{b}\!{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}$	$\log _{10}\!{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5$

Ndryshimi i bazës

Logaritmi $\log _{b}(x)$ mund të llogaritet nga logaritmet mbi x dhe b në lidhje me një bazë arbitrare k duke përdorur formulën e mëposhtme:

$\log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.$

$\log _{b}(x)={\frac {\log _{10}(x)}{\log _{10}(b)}}={\frac {\log _{e}(x)}{\log _{e}(b)}}.$